Some notes about using a prime modulus in a hash function

Modular hashing is a common technique to convert a numeric key into an array index in hash tables. Given a hash function in the form

H(n) = n mod m

it’s stated in many textbooks and articles that using a prime modulus m tends to disperse hash values evenly. One explanation is that “If m is not prime, it may be the case that not all of the bits of the key play a role, which amounts to missing an opportunity to disperse the values evenly” (Sedgewick and Wayne, p. 460). It’s not obvious why this statement holds, since n can be represented as a m-base number (n=∑a_i · mⁱ) and only the last digit plays a role.

Others say that (any) n and m should be co-prime (and a prime m has a better chance). This condition gives evenly distributed hash values, but it’s too strong. For example, if all possible n are evenly distributed, hash values follow an even distribution no matter what m is.

It turns out that the distribution of hash values is related to the greatest common divisor (GCD) of all possible n and m. To demonstrate this, we rewrite the above hash function into

n = a · m + H(n)

where a is a none negative integer. Assuming the GCD of all possible n and m is d, then we have

n = i · d = a · j · d + H(n)

and therefore

H(n) = d · (i - a · j)

Since H(n) has d as a factor, hash values are evenly distributed in range [0, m-1] iff d = 1.

• If all possible n and m are co-prime, then d = 1.
• If n follows a even distribution, then d = 1.
• If the distribution of n is unknown, a prime m increase the probability to minimize d, and thus hash values disperse more evenly.

MongoDB authentication work flow at TCP level

In a personal project I’m looking at ways to manipulate authentication to a MongoDB at communication protocol level. MongoDB clients communicate with the database server using commands that are sent via a TCP/IP socket. Encoding of basic operations including UPDATE, INSERT, QUERY, GET_MORE and KILL_CURSORS are covered in MongoDB Wire Protocol. Authentication, on the other hand, is only described in the official manual at a rather high level. More details of authentication mechanisms are given in MongoDB authentication specifications, but again it’s not clear how authentication messages and commands are encoded at TCP level. After digging around MongoDB core driver with help of its author Christian Kvalheim, I got the flowchart below showing how authentication is done at a low level. Process in the flowchart are linked to source code of MongoDB core driver.

Rational for Church encoding

In λ calculus natural numbers are represented in the following form (following normal order reduction):

0 = λf. λx. x

1 = λf. λx. f x

2 = λf. λx. f (f x)

n = λf. λx. f ⁿ x

Under Church encoding some arithmetic operations are defined as:

[m + n] := λf. λx. (m f) (n f x) = λf. λx. ((m f) · (n f)) x)

[m × n] := λf. m n = m · n

m ⁿ := n m

Note that multiplication is implemented by function composition and exponentiation by reverse function application.

Although Church encoding works fine to represent natural number system, it’s not intuitive where the form λf.λx.f ⁿ x comes from.

Hinze provides a great explanation (twice!). However, for those who finds the above article too long, here’s my clumsy attempt to partially explain the rational behind Church encoding.

In the Peano numeral system, natural numbers are defined using a constant symbol 0 and a unary function symbol S, known as the successor function. 0 is a natural number, and for every natural number n, S(n) is a natural number too. So we can define 1 as S(0), 2 as S(1) = S(S(0)) and so on. This from is the same as the body of λf.λx.f ⁿ x, if we let f = S, x = 0. Now it may become clearer that Church encoding enables a quite straightforward mapping between λ calculus and Peano numerals, that is, given a Church numeral n = λf.λx.f ⁿ x, n S 0 gives you the corresponding Peano numeral.

Y combinator from λ to Javascript

The Y combinator, discovered by Haskell B. Curry, is defined as:

Y = λf. (λx. f (x x))(λx. f (x x))

This form is easy to remember and can be used to derive Y combinator in a functional programming language, like Javascript.

The lambda expression translates to JS as:

However the function body leads to an infinite call loop:

Notice that the two inner functions are the same, so it’s equivalent to:

Now there’s only one x => f(x(x)) so let’s focus on that.

Recall that f expects a (recursive) function. To prevent immediately evaluating x(x) (and thus to prevent the infinite loop), we wrap x(x) in a function that returns the same result for an input n, only when needed.

An example of using Y combinator to construct a recursive function is shown below. Note that ALL functions in the example can be anonymous.

Algorithms behind collaborative editing (part 1)

When preparing for a undergraduate programming class I decided to make a simple Javascript sandbox that allows students to code collaboratively. There were loads of libraries for collaborative editing but I decided to do my own exploration on algorithms that those libraries implement.

A quick search showed two algorithms that are at the core of collaborative editing, difference algorithms (diff) and operational transformation (ot).

A diff algorithm determines the differences between two sequences of symbols (e.g. strings). The basic diff algorithm is described in An O(ND) Difference Algorithm and its Variations by Eugene Myers. This post tries to (re)explain this elegant algorithm.

To understand the diff algorithm we need to firstly introduce the concept of edit graph:

For two sequences S = s₁ s₂ . . . s_N and L = l₁ l₂ . . . l_M , the edit graph for S and L has a vertex at each point in the grid (x, y), x ∈ [0, N] and y ∈ [0, M]. The vertices of the edit graph are connected by horizontal, vertical, and diagonal directed edges to form a directed acyclic graph. Horizontal edges connect each vertex to its right neighbor, i.e. (x−1, y) → (x, y) for x ∈ [1, N] and y ∈ [0, M]. Vertical edges connect each vertex to the neighbor below it, i.e. (x, y−1) → (x, y) for x ∈ [0, N] and y ∈ [1, M]. If s_x = l_y then there is a diagonal edge connecting vertex (x−1, y−1) to vertex (x, y).

As an example, the edit graph of two sequences S = ABCABBA and L = CBABAC is shown below. Thinking of going right as deleting a symbol from S, going down as inserting a symbol, following a diagonal edge as keeping the symbol (or skipping it), then any path from the left upper corner (0, 0) to the right bottom corner (7, 6) gives a sequence of modifications (deletion or insertion) that transform S to L.

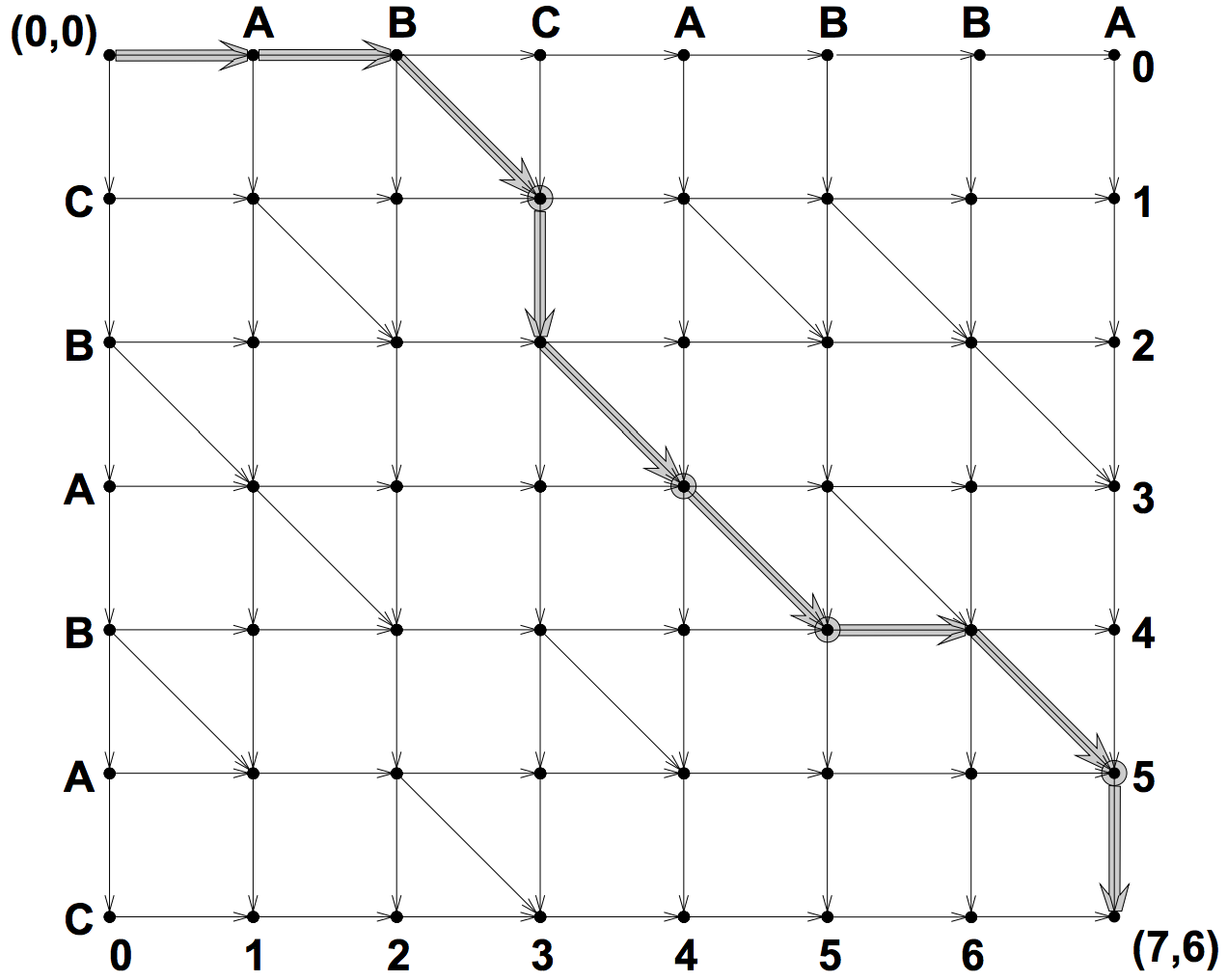
For example, a path go straight right then down, i.e. (0, 0) → (7, 0) → (7, 6), corresponds to the edit sequence [-A, -B, -C, -A, -B, -B, -A, +C, +B, +A, +B, +A, +C], and the bolded path in the edit graph corresponds to the edit sequence [-A, -B, C, +B, A, B, -B, A, +C], where -X denotes deleting the character X, X denotes skipping it, and +X denotes insertion (imagine the cursor starts at the left of S, deletion is to press the Del key, skipping is to press the → key, and insertion is to press the key of the inserted character).

The problem to identify the difference between S and L equals to finding the edit sequence with the minimum number of deletions and insertions together (skipping doesn’t count). This minimum edit sequence is called the Shortest Edit Script (SES) that converts sequence S into sequence L. In the above examples, the first edit sequence has 7 deletions and 6 insertions, while the second has 3 deletions and 2 insertions. It turns out that the second edit sequence has the minimum total number of deletions and insertions (5) and thus it’s a SES (there can be more than one SES) of S and L.

Since the total number of edits cannot not exceed the sum of the length of the two sequences, minimising the number of edits is the same as skipping as many symbols as possible.

Let D be the number of insertions and deletions of a path, L be the number of diagonal edges of the path, and N and M be the length of the two sequences of symbols respectively, we have D = N + M - 2L.

Actually finding a SES is the same as finding the longest subsequence of symbols from S and L that are 1) common between the two sequences, and 2) in the same order in each sequence. This subsequence is called the longest common subsequence (LCS) of S and L. It is distinct from the Longest Common Substring, which has to be contiguous. Again, multiple LCSs may exist for two sequences. In the case of S and L, a LCS is CABA.

The definition of LCS implies that in the edit graph LCS consists of only diagonal edges (shared symbols) that belong to the same path (keeping the order).

Give diagonal edges weight 0 and non-diagonal edges weight 1. The LCS/SES problem is equivalent to finding a minimum-cost path from (0, 0) to (N, M) in the weighted edit graph and is thus a special instance of the single-source shortest path problem. However a general shortest path algorithm isn’t efficient in this specific case. There’s no need to traverse all vertices of the edit graph, as shown by the algorithm below.

Now some definitions to help understand the diff algorithm.

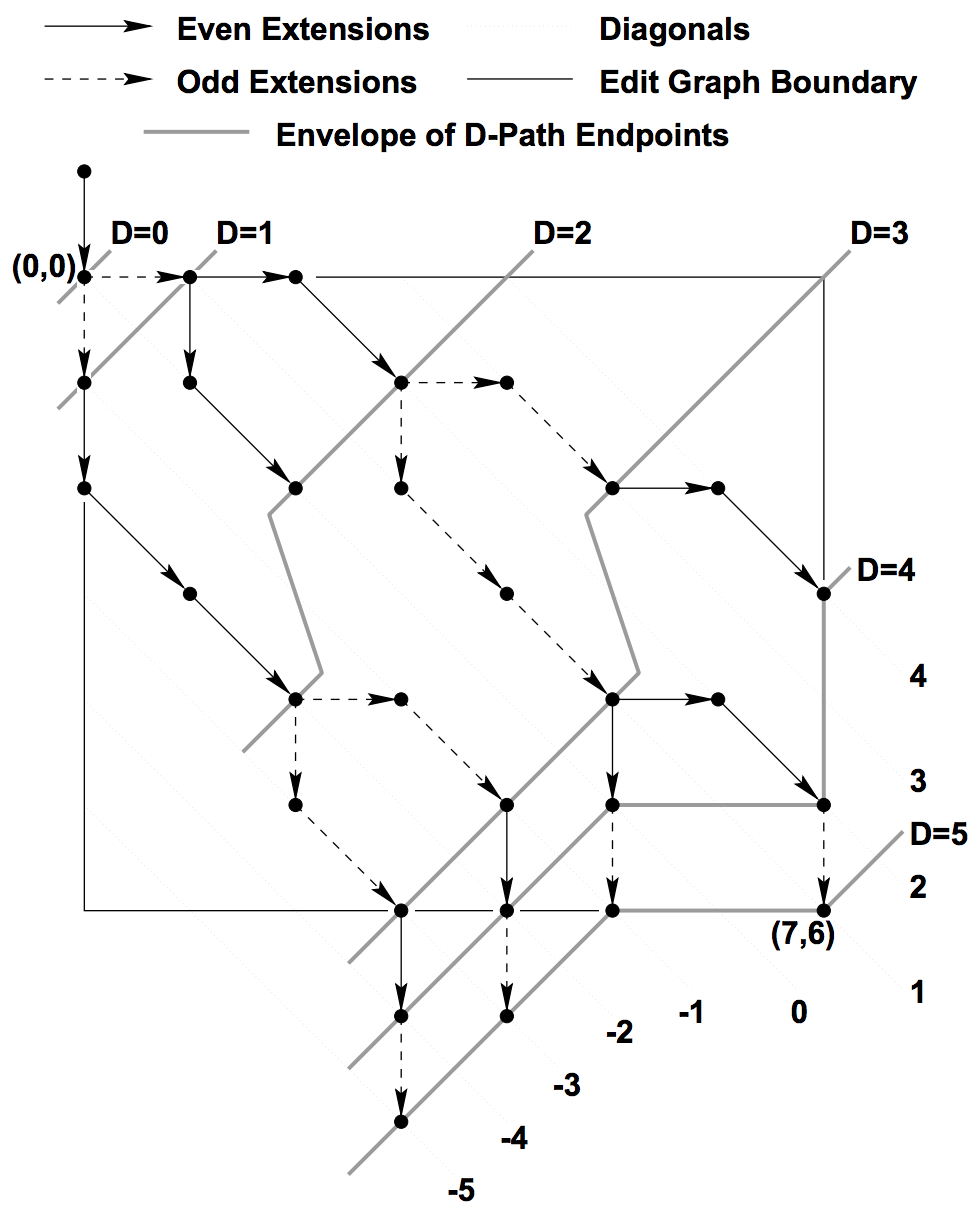
• diagonal k In the edit graph all points (x, y) for which x - y = k lie on a diagonal line, and we call it diagonal k, where k ∈ [-M, N] (left-bottom is on diagonal -M and right-up is on diagonal N).

• D-path A D-path is path starting at (0, 0) that has exactly D non-diagonal edges. A D-path must consists of a prefix (D-1)-path followed by a horizontal or vertical edge and 0 or more continuous diagonal edges.

Intuitively the algorithm starts with point (0, 0), which is on 0-path, and iteratively finds the furthest endpoints of 1-path, 2-path (named envelop of D-path endpoints) etc., until point (N, M) is reached, as shown in the figure.

This procedure looks like the following Javascript code.

Now let’s figure out how to find furthest D-path endpoints. A D-path can only end on k diagonals for those k ∈ {−D, −D +2, . . . D−2, D}. Assuming furthest D-path endpoints are stored in an array V, for which V[k] gives the endpoint of the D-path on diagonal k, V would look like V[-D], V[-D+2], …, V[D-2]. For an endpoint (x, y) we store only x in V, i.e. V[k] = x, and y can be computed as x - k (definition of diagonal k).

The furthest endpoint of (D+1)-path on diagonal k can be reached by either moving right one step from the furthest D-path endpoint on diagonal k-1 (V[k-1]) and then following diagonal edges on diagonal k as far as possible, or moving down one step from diagonal k+1 (V[k+1]).

The furthest D-path endpoints and (D+1)-path endpoints are on disjoint diagonals. Therefore they can co-exist in V in each iteration of finding furthest (D+1)-path endpoints.

The code for the above procedure is shown below:

The code above gives the length of a SES, but there’s no way to construct the SES (since V only stores vertices of the most recent two iterations). In the paper it keeps a copy of V in each iteration. Let V_D be the furthest endpoints of D-paths, for an end point V_D[k], it is straightforward to determine whether V_D-1[k+1] leads to V_D[k], and thus includes a vertical edge or a horizontal edge followed by diagonal edges in the SES.

In this article I’m going to use a different approach. A vertex is presented as a data structure containing its coordinates and a link pointing back to the vertex that lead to this vertex. This structure enables us to restore the SES from its endpoint via backtracking. The modified diff algorithm is shown below.

diff('ABCABBA', 'CBABAC') gives [“-A”, “-B”, “C”, “+B”, “A”, “B”, “-B”, “A”, “+C”].